Sử dụng thống kê để xác định và loại bỏ dữ liệu ngoại lai cho machine learning trong R và Python

Nguồn ảnh

Outliers (dữ liệu ngoại lai hay là nhiễu) là một trong những thuật ngữ được sử dụng rất rộng rãi trong thế giới data science. Trong quá trình xây dựng các mô hình dự đoán, việc xác định và loại bỏ outliers trong dữ liệu là một bước vô cùng quan trọng. Nó giúp tăng cao độ chính xác cho các mô hình dự đoán.

Khi phân tích, chúng ta thường dùng các tham số như là mean, median và mode để biết xu hướng tập trung của dữ liệu. Tuy nhiên, một câu hỏi quan trọng cần phải trả lời khi xem xét chất lượng của một mẫu dữ liệu trong phân tích đó là “làm sao để đo được độ biến động (hay độ phân tán) của mẫu dữ liệu đó”?. Vì chúng ta có thể có 2 mẫu dữ liệu với cùng giá trị mean nhưng độ biến động của chúng lại hoàn toàn khác nhau. Trong thống kê những đại lượng phổ biến nhất để đo lường tiêu chí này là khoảng phần tư (interquartile range, IQR) (hay còn được gọi là khoảng cách giữa các tứ phân vị), phương sai (variance) và độ lệch chuẩn (standard deviation, STD).

Ở post này tôi sẽ giới thiệu với các bạn cách sử dụng 2 phương pháp thống kê trong R và Python để xác định và loại bỏ outliers trong dữ liệu đó là:

1. STD có thể sử dụng để xác định outliers trong dữ liệu có dạng/gần như dạng phân phối chuẩn (hay còn gọi là phân phối Gauss)
2. IQR có thể sử dụng để xác định và loại bỏ outliers không phụ thuộc vào dạng phân phối của dữ liệu.

Và ở cuối post tôi sẽ hướng dẫn các bạn viết hàm tự động xác định và loại bỏ outliers từ dữ liệu sử dụng hai phương pháp trên.

1. Tạo dữ liệu để thực hành

Để thực hành tôi sử dụng hàm mô phỏng phân phối chuẩn rnorm() trong R để tạo ra dãy số ngẫu nhiên gồm 5000 số với các tham số giá trị trung bình là 20 và độ lệnh chuẩn là 2 như sau:

# R
data = rnorm(5000, mean = 20, sd = 2)

Với Python thì ta thực hiện như sau:

Trước hết cần nạp thư viện reticulate để sử dụng Python trong R:

# R
library(reticulate)

Cụ thể về cách sử dụng thư viện reticulate để kết hợp R và Python tôi đã giới thiệu ở post trước, các bạn có thể đọc ở đây

Tạo dữ liệu trong python:

# Python
# Tạo dữ liệu tương tự như trong R
from numpy.random import randn
data = 2* randn(5000) + 20

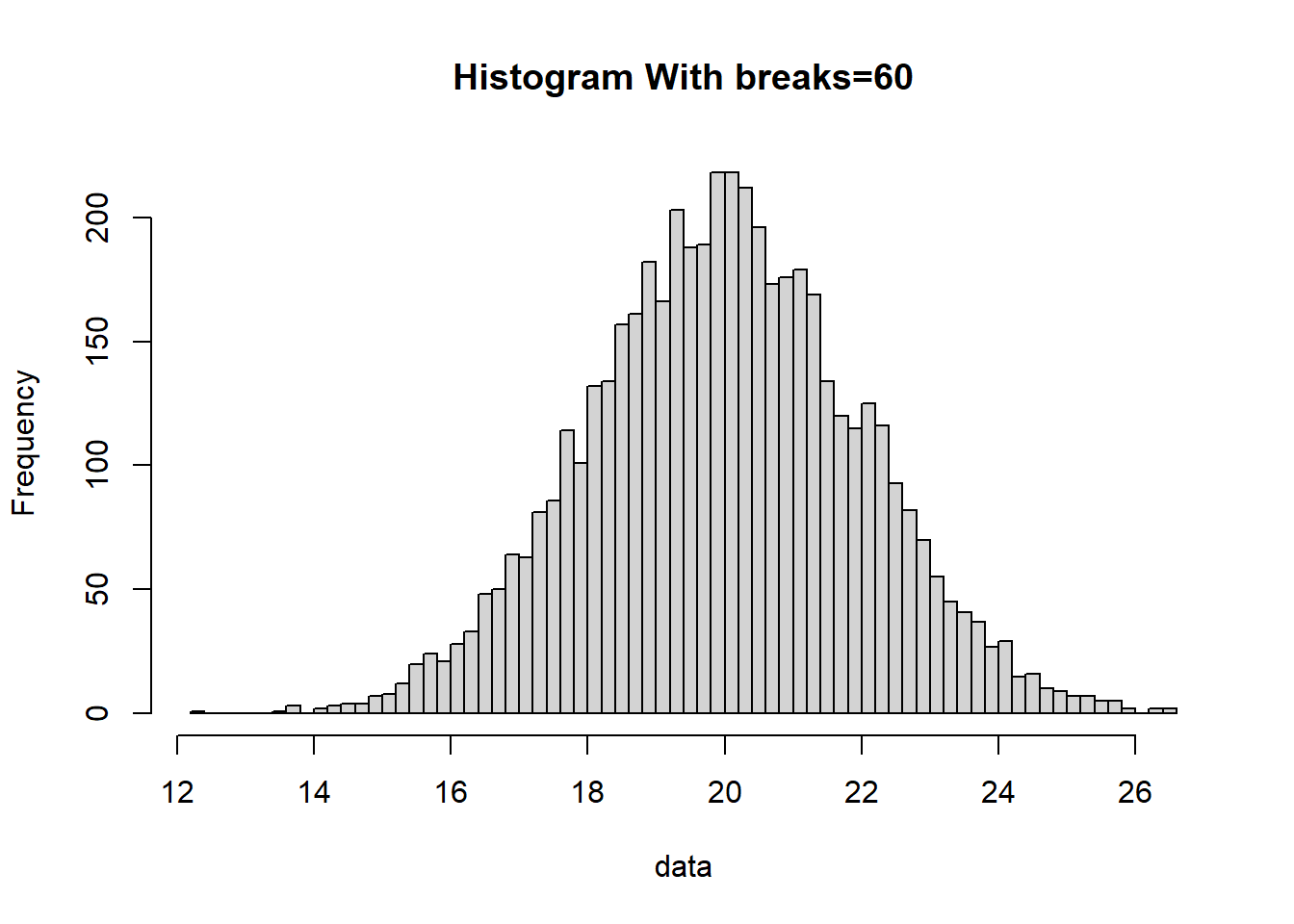
Trong dữ liệu được tạo ra từ phân phối chuẩn sẽ có một số giá trị nằm cách xa giá trị trung bình mean mà chúng ta có thể xác định là outliers.

Biểu diễn dữ liệu bằng histogam sử dụng hàm hist():

# R
hist(data, breaks= 60, main="Histogram With breaks=60")

Nhân tiện đây tôi cũng xin giới thiệu một số hàm hỗ trợ cho các tính toán thống kê trong R như: summary(), sample(), dnorm(), pnorm(), qnorm(), dunif(), punif(), qunif(), runif(), mean(), sd(), cov(), cor(),…

Hàm summay() cho phép thực hiện thống kê mô tả (descriptive statistics) để cung cấp cho chúng ta một số thông tin thống kê cơ bản về một biến số:

# R
summary(data)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   12.32   18.66   19.99   19.99   21.30   26.54

Ví dụ sử dụng hàm sample() để tạo mẫu ngẫu nhiên có lặp lại 10 số nguyên từ 0 đến 9:

# R
sample(0:9, replace = TRUE)

##  [1] 6 6 0 9 7 1 6 6 8 4

Ví dụ sử dụng hàm tính mật độ phân phối chuẩn dnorm() để ước tính xác xuất của học sinh có điểm là 16.5 biết rằng điểm của học sinh tuân theo phân phối chuẩn với giá trị trung bình là 15, độ lệnh chuẩn là 2.5:

# R
dnorm(16.5, mean = 15, sd = 2.5)

## [1] 0.1332898

Tiếp theo ví dụ trên để ước tính xác suất học sinh có điểm tối thiểu là 16.5, ta có thể sử dụng hàm tính xác suất chuẩn tích lũy pnorm() như sau:

# R
1 - pnorm(16.5, mean = 15, sd = 2.5)

## [1] 0.2742531

Chức năng của các hàm R còn lại cũng như các hàm tương tự trong Python các bạn có thể tự tìm hiểu thêm.

2. Phương pháp STD

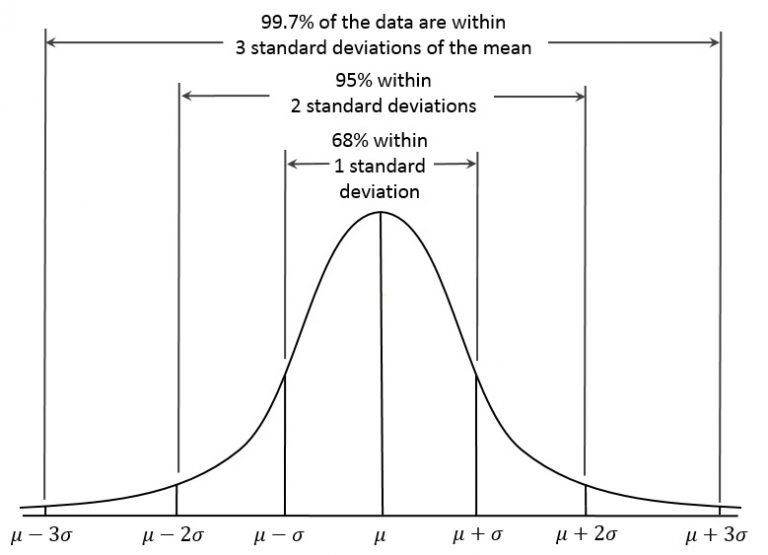
Nếu như biết được rằng dữ liệu có dạng phân phối Gauss thì chúng ta có thể sử dụng STD trong vài trò là thước đo giới hạn độ phân tán của dữ liệu để xác định outliers.

Trong phân phối Gauss dựa vào giá trị trung bình mean và STD cho phép chúng ta kiểm tra được độ phân tán (hay là phần trăm bao phủ) của dữ liệu đó như thế nào. Ví dụ:

• Độ bao phủ với 1 STD từ mean là 68%
• Độ bao phủ với 2 STD từ mean là 95%
• Độ bao phủ với 3 STD từ mean là 99.7%

Nguồn ảnh

Vậy nên với dữ liệu dạng Gauss có độ phân tán bình thường thì với 3STD, chúng ta sẽ bao phủ được khoảng > 99% của dữ liệu. Từ đó những điểm dữ liệu nằm ngoài 3STD sẽ được coi là outliers.

Các bước xác định outliers bằng phương pháp STD như sau:

Bước 1: Tính mean và std

# tính mean và std
# R
mean_data <- mean(data)
std_data <- sd(data)

# Python
from numpy import mean
from numpy import std
mean_data, std_data = mean(data), std(data)

Bước 2: Tính giá trị biên Upper/Lower để xác định outliers

# thiết lập giới hạn để xác định outliers
# R
limit_std = 3*std_data
lower_std = mean_data - limit_std
upper_std = mean_data + limit_std

# Python
limit_std = 3*std_data
lower_std, upper_std = mean_data - limit_std, mean_data + limit_std

Bước 3: Xác định và loại bỏ outliers dựa trên giá trị biên

# xác định outliers
# R
ouliers_index_std <- which(data > upper_std | data < lower_std)
print(paste("Number of outliers:", length(ouliers_index_std)))

## [1] "Number of outliers: 11"

# Python
ouliers_index_std = [x for x in data if x < lower_std or x > upper_std]
print('Number of outliers: %d' % len(ouliers_index_std))

## Number of outliers: 13

# Loại bỏ outliers
# R
data_new_std <- data[-ouliers_index_std]
print(paste("Number of Non-outliers:", length(data_new_std)))

## [1] "Number of Non-outliers: 4989"

# Python
data_new_std = [x for x in data if x >= lower_std and x <= upper_std]
print('Number of Non-outliers:: %d' % len(data_new_std))

## Number of Non-outliers:: 4987

2. Phương pháp IQR

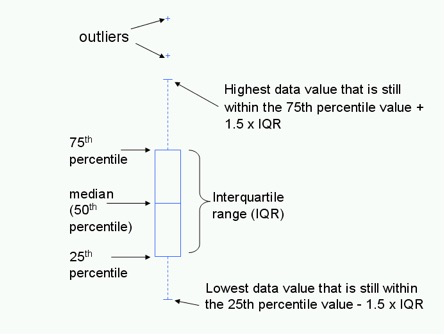
Tứ phân vị là đại lượng mô tả sự phân bố và sự phân tán của tập dữ liệu. Tứ phân vị có 3 giá trị, đó là tứ phân vị thứ nhất Q1 (25th), thứ hai Q2 (50th) hay median, và thứ ba Q3 (75th). Ba giá trị này chia một tập hợp dữ liệu (đã sắp xếp dữ liệu theo trật từ từ bé đến lớn) thành 4 phần có số lượng quan sát đều nhau. Tứ phân vị được xác định như sau:

• Sắp xếp các số theo thứ tự tăng dần
• Cắt dãy số thành 4 phàn bằng nhau
• Tứ phân vị là các giá trị tại vị trí cắt

Nguồn ảnh

IQR là sự khác biệt giữa tứ phân vị thứ nhất Q1 và tứ phân vị thứ ba Q3:

$$IQR = Q_3 - Q_1$$

Giá trị IQR có thể sử dụng để xác định outliers bằng cách thiết lập các giá trị biên Upper/Lower giống với phương pháp STD như sau: Nếu chúng ta trừ đi kxIQR từ tứ phân vị đầu tiên Q1, bất kỳ giá trị dữ liệu nào nhỏ hơn con số này được coi là giá trị outliers. Tương tự như vậy, nếu chúng ta thêm kxIQR đến tứ phân vị thứ ba Q3, bất kỳ giá trị dữ liệu nào lớn hơn con số này được coi là outliers. Giá trị k thường được chọn là 1.5. Trong trường hợp xác định các extreme outliers có thể dùng giá trị k = 3.

Các bước xác định outliers bằng phương pháp IQR:

Bước 1: Tính IQR

# Tính IQR
# R
q25 <- quantile(data, 0.25)
q75 <- quantile(data, 0.75)
iqr <- q75 - q25

# Python
import numpy as np
q25, q75 = np.percentile(data, 25), np.percentile(data, 75)
iqr = q75 - q25

Bước 2: Tính giá trị biên Upper/Lower để xác định outliers

# thiết lập giới hạn để xác định outliers
# R
limit_iqr = 1.5*iqr
lower_iqr = q25 - limit_iqr
upper_iqr = q75 + limit_iqr

# Python
limit_iqr = 1.5*iqr
lower_iqr, upper_iqr = q25 - limit_iqr, q75 + limit_iqr

Bước 3: Xác định và loại bỏ outliers dựa trên giá trị biên

# xác định outliers
# R
ouliers_index_iqr <- which(data > upper_iqr | data < lower_iqr)
print(paste("Number of outliers:", length(ouliers_index_iqr)))

## [1] "Number of outliers: 37"

# Python
ouliers_index_iqr = [x for x in data if x < lower_iqr or x > upper_iqr]
print('Number of outliers: %d' % len(ouliers_index_iqr))

## Number of outliers: 39

# Loại bỏ outliers
# R
data_new_iqr <- data[-ouliers_index_iqr]
print(paste("Number of Non-outliers:", length(data_new_iqr)))

## [1] "Number of Non-outliers: 4963"

# Python
data_new_iqr = [x for x in data if x >= lower_iqr and x <= upper_iqr]
print('Non-outlier observations: %d' % len(data_new_iqr))

## Non-outlier observations: 4961

3. Xây dựng hàm tự động xác định và loại bỏ outliers

Chúng ta có thể tạo một hàm trên R dựa vào các bước ở trên để tự động xác định và xóa outliers như sau:

# R
# Tạo hàm tự động xác định và loại bỏ outliers bằng phương pháp STD
find_outliers_std <- function(data) {
  # tính giá trị biên Upper/Lower
  mean_data <- mean(data)
  std_data <- sd(data)
  limit = 3*std_data
  lower = mean_data - limit
  upper = mean_data + limit
  # xác định outliers
  ouliers_index <- which(data > upper | data < lower)
  # Thông báo thông tin về các outliers đã xóa
  if (length(ouliers_index) > 0 ) {
    message(paste("Number of outliers:", length(ouliers_index)))
    message(paste("Number of Non-outliers:", length(data_new_iqr)))
  # return the data with the outliers removed
  return(data[-ouliers_index])
  } else {
    message("Not outliers")
  }
}

Tương tự ta có thể tạo hàm xác định outliers bằng phương pháp IQR như sau:

# Python
# Tạo hàm tự động xác định và loại bỏ outliers bằng phương pháp IQR
find_outliers_iqr <- function(data) {
  # Tính IQR
  q25 <- quantile(data)[2]
  q75 <- quantile(data)[4]
  iqr = q75 - q25 
  # Tính giá trị biên Upper/Lower để xác định outliers
  upper = q75 + iqr * 1.5
  lower = q25 - iqr * 1.5
  # xác định outliers
  ouliers_index <- which(data > upper | data < lower)
  # Thông báo thông tin về các outliers đã xóa
  if (length(ouliers_index) > 0 ) {
    message(paste("Number of outliers:", length(ouliers_index)))
    message(paste("Number of Non-outliers:", length(data_new_iqr)))
  # return the data with the outliers removed
  # return the data with the outliers removed
  return(data[-ouliers_index])
  } else {
    message("Not outliers")
  }
}

Kiểm tra kết quả thực hiện của hai hàm này:

new_data_std <- find_outliers_std(data)

## Number of outliers: 11

## Number of Non-outliers: 4963

new_data_iqr <- find_outliers_iqr(data)

## Number of outliers: 37

## Number of Non-outliers: 4963

Đối với Python thì các bạn có thể tạo hàm tương tự sử dụng các bước trên